Duncan's SuDoku Solver

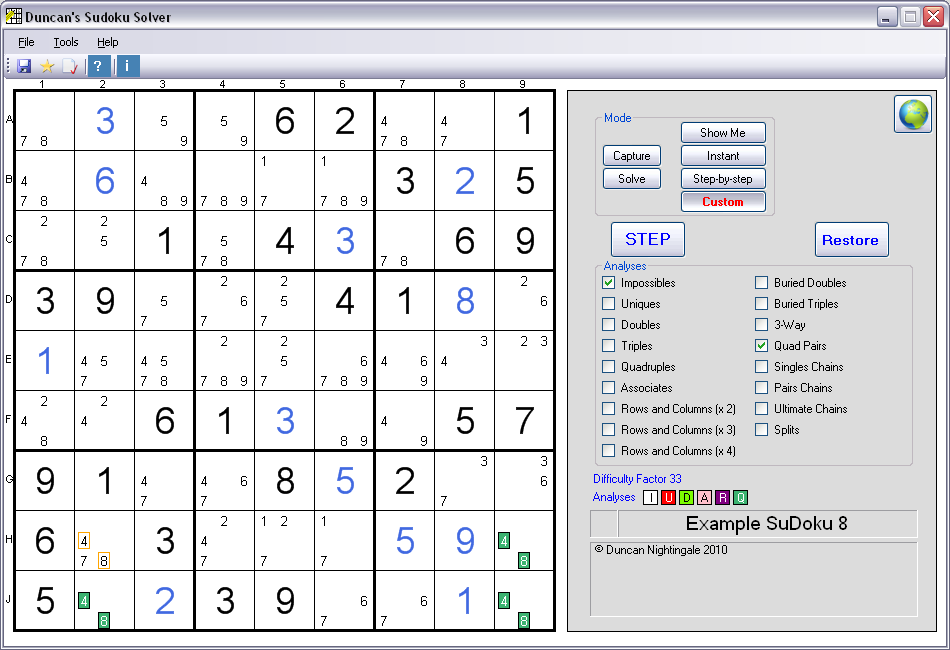
This is a version 8.4 screenshot

Quad Pair:

Four Squares each containing a Pair arranged in a rectangle so that they share two Rows , two Columns and two Boxes .

In this example the four Pairs (coloured sea green) are on H9, J2, J9 and (possibly) H2. If H2 were to contain the same Pair (4 and 8), then the SuDoku would not have a unique solution.

To understand why this is true, consider the effect of H2 being a 4. This would force H9 and J2 to be an 8 and force J9 to be a 4. This would eliminate all other 4s and 8s in the same two Rows, Columns and Boxes. Now consider the effect of H2 being an 8. H9 and J2 would be a 4 and J9 would be an 8 - but once again all other 4s and 8s in the same two Rows, Columns and Boxes would be eliminated. In other words, the effect on the rest of the SuDoku is identical - irrespective of whether H2 is a 4 or an 8. So there would be two solutions to this SuDoku, because interchanging the 4s and 8s in the four Squares would have no effect on the rest of the SuDoku. Since SuDokus are assumed to have a unique solution, this cannot be allowed to happen - the Quad Pairs arrangement is an impossible scenario. Therefore 4 and 8 in H2 (outlined in orange) are impossible Solutions and can be eliminated.

For this logic to work, the four Squares must share only two Columns, two Rows and two Boxes. If they shared four Boxes (for example if the four Squares were F2, F9, J2 and J9), then the logic would not be the same - because eliminations in the rest of the SuDoku would be different depending on which Boxes the 4s and 8s were in - so the 4s and 8s would not be interchangeable.

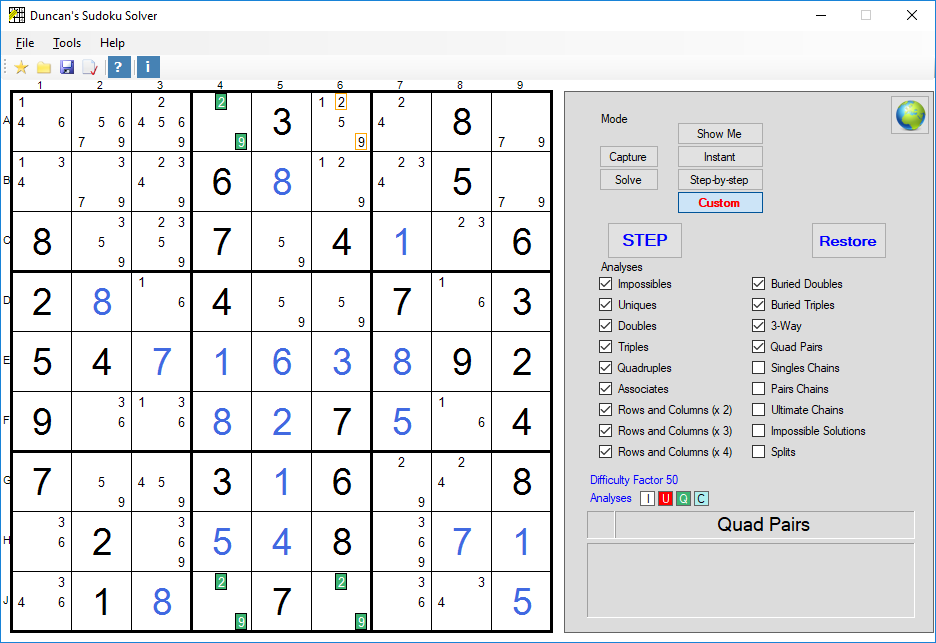
This is a version 10.1 screenshot

Quad Pair:

In this 2nd example there is more than one 'extra' possible in the target Square (A6), but the logic is still the same and 2 and 9 can be removed from A6.

This variant (more than one extra possible) requires version 10.1 or later.

© Duncan Nightingale 2024