Example of an Ultimate Chain
- aka "Alternating Inference Chain"
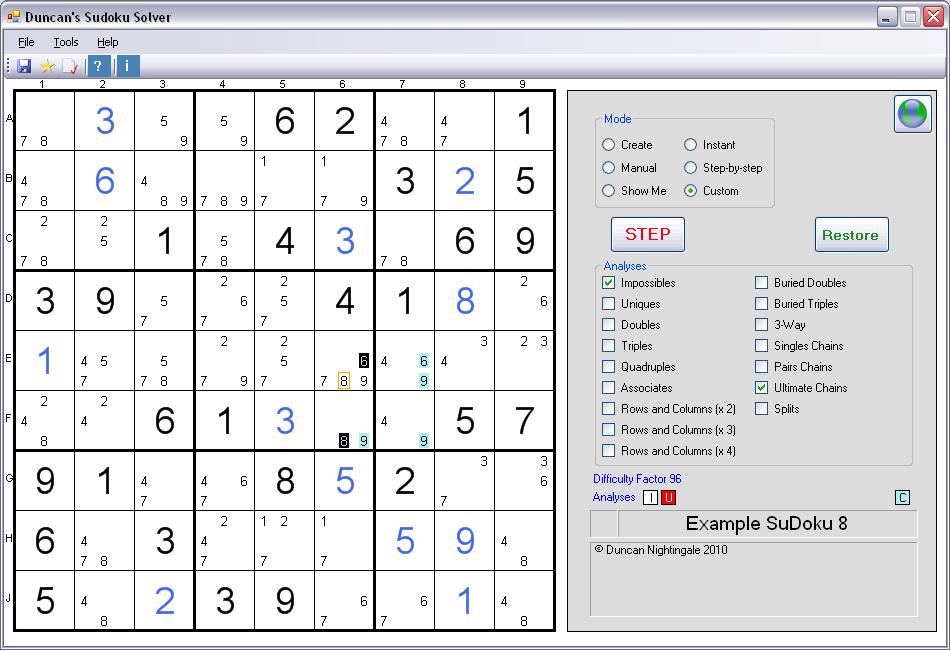
This is a screenshot
Ultimate Chain:
A linked Chain of
Possibles. The links (coloured pale blue) may be made in a number of different ways
but always such that if either of the ends (coloured black) is 'false', then the other must be 'true' and vice-versa - causing some Possibles to be
removable.Not just Ultimate Chains, but the ultimate Analysis! Many of the other Analyses (Doubles, Rows and Columns, Singles Chains and Pairs Chains) are subsets of Ultimate Chains - once it is deployed the other Analyses are rarely needed. However, it is an Analysis that is very difficult (but not impossible) for a 'human' to use. So, with Ultimate Chains you are crossing over a line that most people would draw between 'the toughest SuDoku for humans' and 'for computer solvers only'!
On this website, only ULTIMATE SuDokus require the Ultimate Chains Analysis to solve them. The other levels - BEGINNER, EASY, TRICKY, DIFFICULT and CHALLENGING can all be solved using the other Analyses. Only if you are looking for the toughest of challenges - or you are testing your own computer solver - should you read on!
In this example, the Ultimate Chain has ends with values 8 (F6) and 6 (E6), coloured black. The linking elements are coloured pale blue. The logic is as follows:
If the first end (F6) is NOT an 8,
then it (F6) MUST be a 9,
and the next link (F7) CANNOT be a 9,
and the next link (E7) MUST be a 9,
so it (E7) CANNOT be a 6,
and the end of the chain (E6) MUST be a 6,
which means it (E6) CANNOT be an 8.
The 'MUST be' links are caused by there only being two Possibles of the same value in the relevant Row, Column, or Box - or caused by there only being two Possibles in the Square.
The 'CANNOT be' links are caused by the normal SuDoku rule that Solution values cannot be repeated in the same Row, Column, or Box - or caused by the Square already having another Solution.
All this means that if F6 is an 8, then E6 cannot be an 8; and if F6 is NOT an 8, then E6 still cannot be an 8. So the 8 in E6 (outlined in orange) is impossible and can be removed.
Second Example of an Ultimate Chain
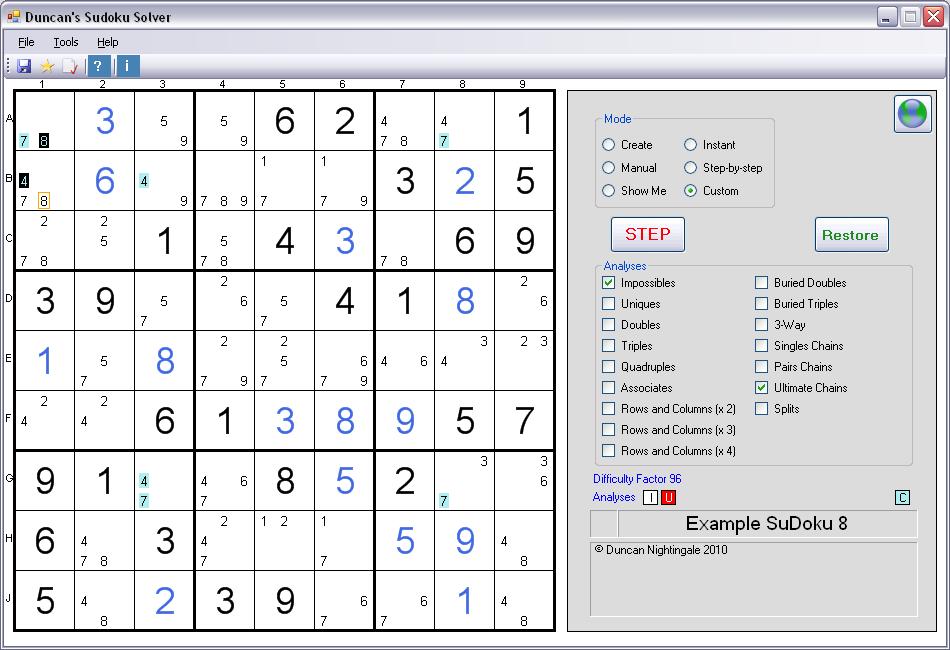
This is a screenshot
In this second example, the Ultimate Chain has ends with values 8 (A1) and 4 (B1), coloured black. As before, the linking
elements are coloured pale blue. The logic is as follows:If the first end (A1) is NOT an 8,
then it (A1) MUST be a 7,
and the next link (A8) CANNOT be a 7,
and the next link (G8) MUST be a 7,
and the next link (G3) CANNOT be a 7,
so it (G3) MUST be a 4,
and the next link (B3) CANNOT be a 4,
and the end of the chain (B1) MUST be a 4,
which means it (B1) CANNOT be an 8.
The 'MUST be' links are caused by there only being two Possibles of the same value in the relevant Row, Column, or Box - or caused by there only being two Possibles in the Square.
The 'CANNOT be' links are caused by the normal SuDoku rule that Solution values cannot be repeated in the same Row, Column, or Box - or caused by the Square already having another Solution.
All this means that if A1 is an 8, then B1 cannot be an 8; and if A1 is NOT an 8, then B1 still cannot be an 8. So the 8 in B1 (outlined in orange) is impossible and can be removed.