Duncan's SuDoku Solver

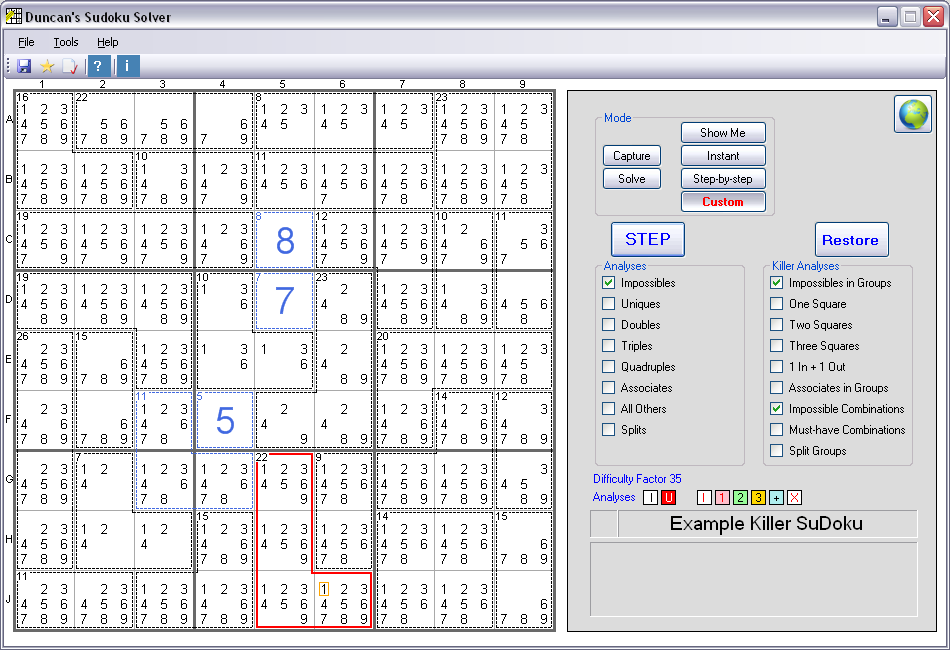
This is a version 8.4 screenshot

Impossible Combinations:

Possible Solutions that can be eliminated due to restrictions imposed by the Group they are in, or by other Groups in the same Row, Column, or Box.

In this example the Group outlined in red contains four Squares which must add up to 22. If J6 is a 1, then the other three Squares must add up to 21, which is impossible due to the lack of 7s and 8s - so the 1 on J6 is impossible and can be eliminated.

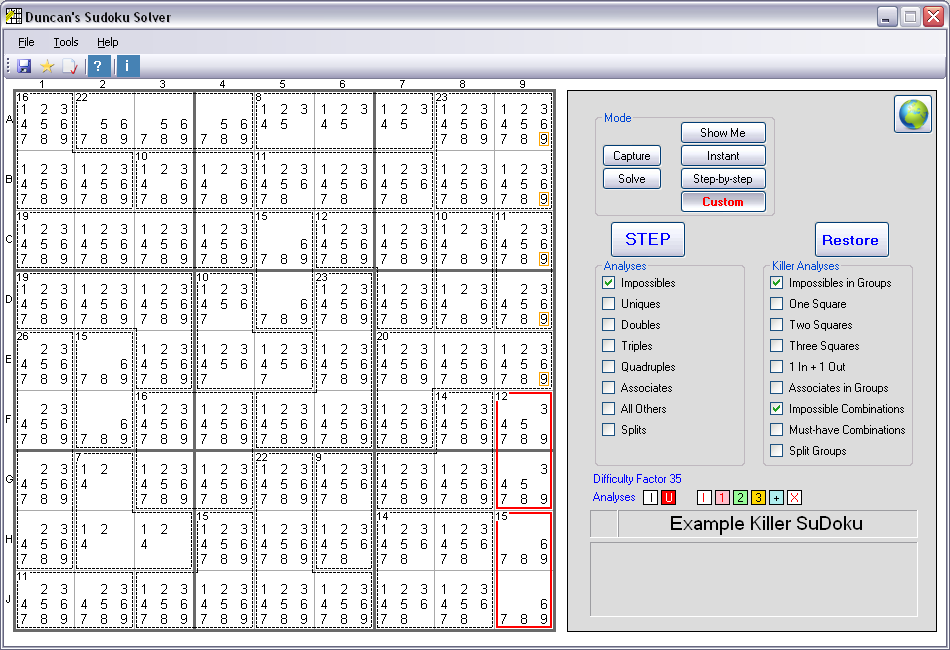
This is a version 9.0 screenshot

In this second example, there are two Groups of two Squares - both of which are in the same Column. The first Group (F9 and G9) must add up to 12, which means possible combinations of Solutions are: 3/9, 4/8 or 5/7. The second Group (H9 and J9) must add up to 15, which means possible combinations of Solutions are: 6/9 or 7/8. If the second Group turns out to be 7/8, then the first Group must be a 3/9 (due to elimination of all other 7s and 8s in the same Column). If, on the other hand, the second Group turns out to be 6/9, there can be no other 9s in the same Column. Either way, the 9s in A9, B9, C9, D9 and E9 are impossible and can be eliminated.

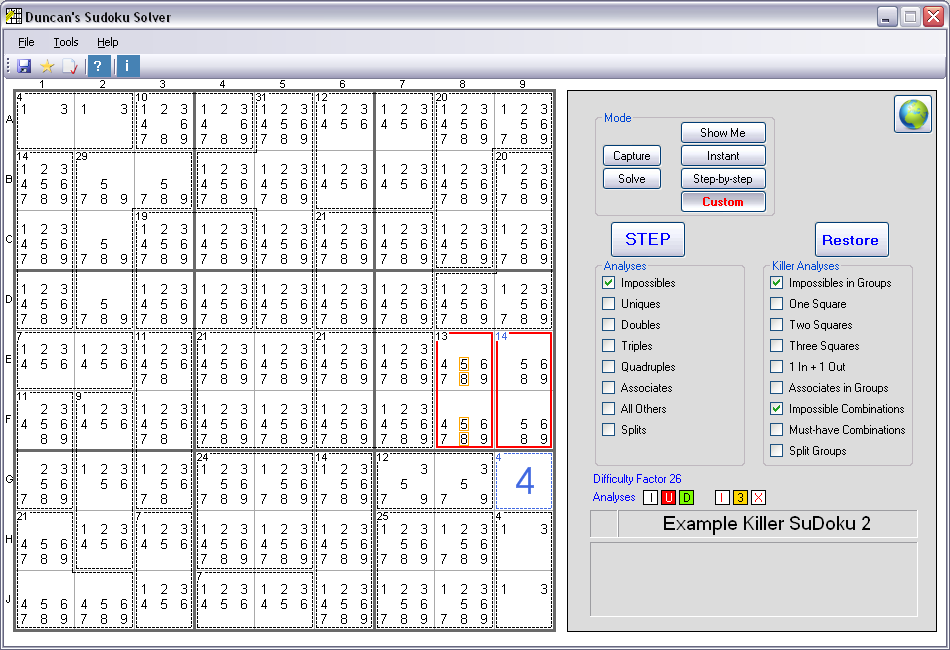
This is a version 9.0 screenshot

In this third example, there are two Groups of two Squares - both of which are in the same Box. The first Group (E8 and F8) must add up to 13, which means possible combinations of Solutions are: 4/9, 5/8 or 6/7. The second Group (E9 and F9) must add up to 14, which means possible combinations of Solutions are: 5/9 or 6/8. If the second Group turns out to be 5/9, then the first Group cannot be 5/8 (due to elimination of all other 5s and 9s in the same Box). If, on the other hand, the second Group turns out to be 6/8, then the first Group also cannot be 5/8 (due to the elimination of all other 6s and 8s in the same Box. Either way, the first Group cannot be 5/8, so the 5s and 8s in E8 and F8 are impossible and can be eliminated.

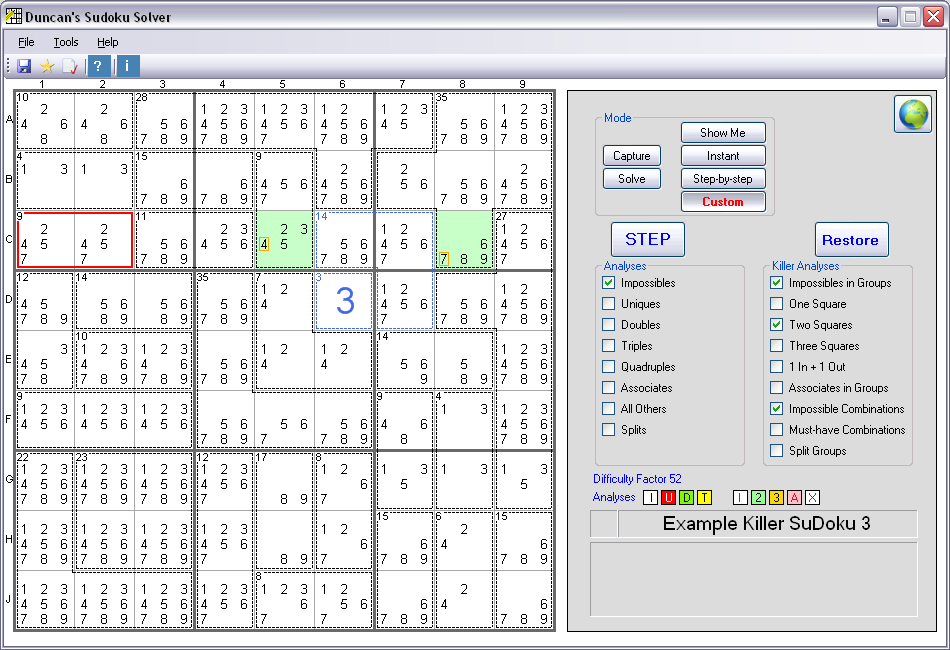
This is a version 9.0 screenshot

In this fourth example, there are also two Groups of two Squares - similar to the pevious example. But now the 'Impossible Combinations' analysis is working in conjunction with the 'Two Squares' analysis - so the second 'group' is actually two odd Squares with a known total, rather than a Group in its own right (the 'Two Squares' analysis is looking at Rows A and B to work this out). The first Group (C1 and C2, outlined in red) must add up to 9, which means possible combinations of Solutions are: 2/7 or 4/5. The second 'group' (C5 and C8, whole Squares coloured green) must add up to 11, which means possible combinations of Solutions are: 2/9, 3/8, 4/7 or 5/6. If the first Group turns out to be 2/7, then the second 'group' cannot be 4/7 (due to elimination of all other 2s and 7s in the same Row). If, on the other hand, the first Group turns out to be 4/5, then the second 'group' also cannot be 4/7 (due to the elimination of all other 4s and 5s in the same Row). Either way, the second 'group' cannot be 4/7, so the 4 and 7 in C5 and C8 are impossible and can be eliminated.

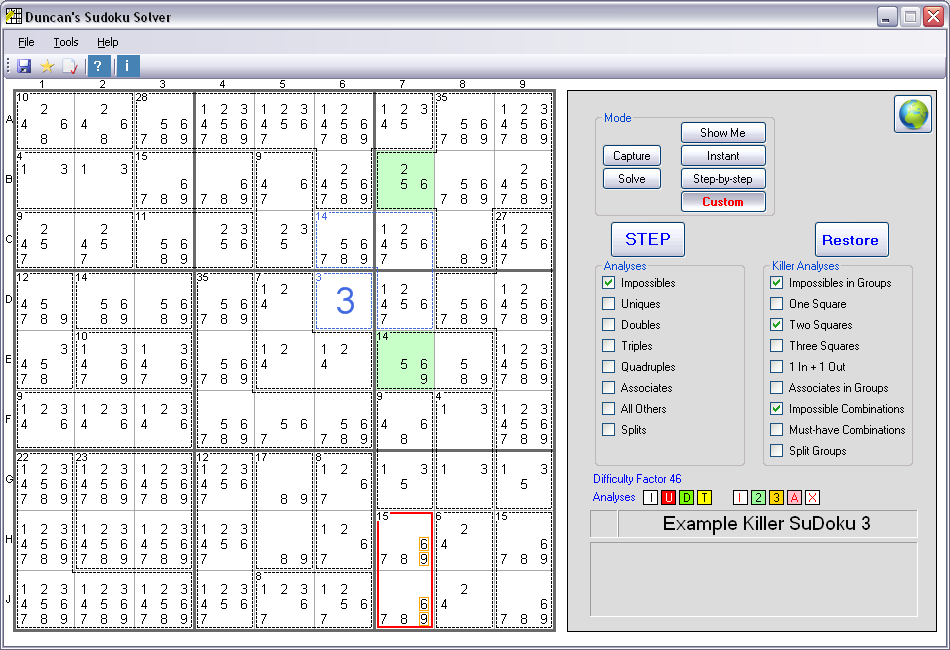
This is a version 9.0 screenshot

In this fifth example, there are also two Groups of two Squares - similar to the previous example. This time the 'Two Squares' analysis is looking at Columns 8 and 9 to work out that the Squares B7 and E7 must add up to 11 - so possible combinations of Solutions are: 2/9 or 5/6. The second Group (H7 and J7, outlined in red) must add up to 15, which means possible combinations of Solutions are: 6/9 or 7/8. If the second Group were to be 6/9, then both possible combinations for the first 'group' (2/9 and 5/6) would be eliminated, which is impossible. So the second Group must be 7/8 and the 6s and 9s in H7 and J7 can be eliminated

© Duncan Nightingale 2024