Example of a 3-Way
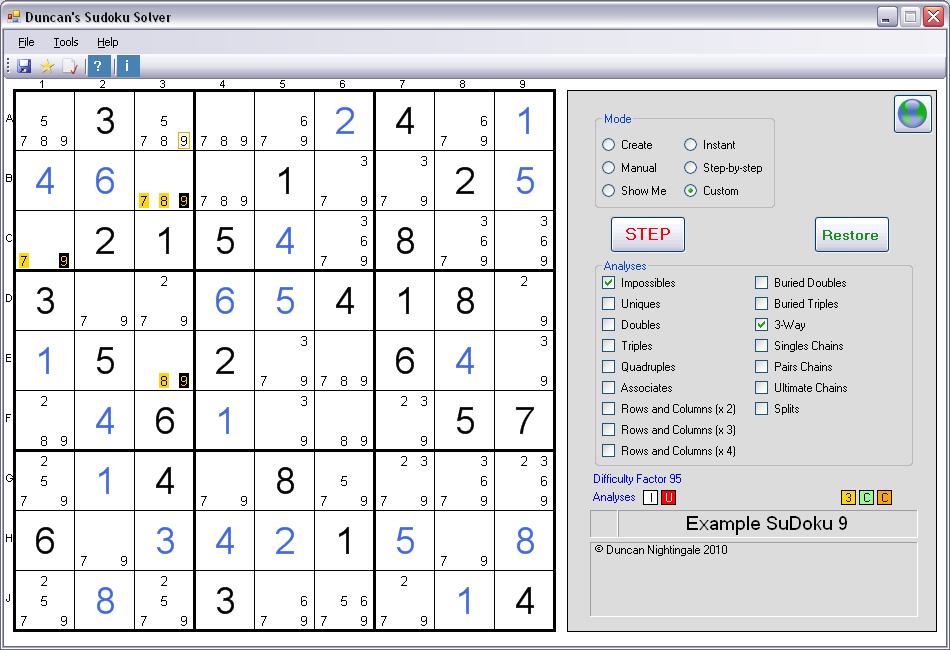
This is a screenshot
3-Way:
Three Squares containing three different
Possibles between them. One Square contains all three Possibles, the other two
Squares contain two different Pairs. The common Possible to all three Squares is coloured black. The other Possibles in the arrangement are
coloured gold. Any Possible that can 'see' all three common Possibles can be removed. For a Possible to 'see' another Possible, it must
simply be in the same
Row,
Column,
or Box and have the same value.In this example, the Square containing three Possibles is B3 and the two Pairs are C1 and E3. The 9 on A3 can 'see' all three common Possible (coloured black).
Consider the Solution to C1. If it is a 9, then the 9 on A3 is impossible. If it is a 7, then B3 and E3 become a Double (with just 8 and 9 left in each Square). This means 8 and 9 are impossible anywhere else in Column 3 - including the 9 on A3 which may be removed.
Alternatively, consider the Solution to E3. If it is a 9, then the 9 on A3 is impossible. If it is an 8, then B3 and C1 become a Double (with just 7 and 9 left in each Square). This means 7 and 9 are impossible anywhere else in the top-left Box - including the 9 on A3 which may be removed.