Example of a Singles Chain
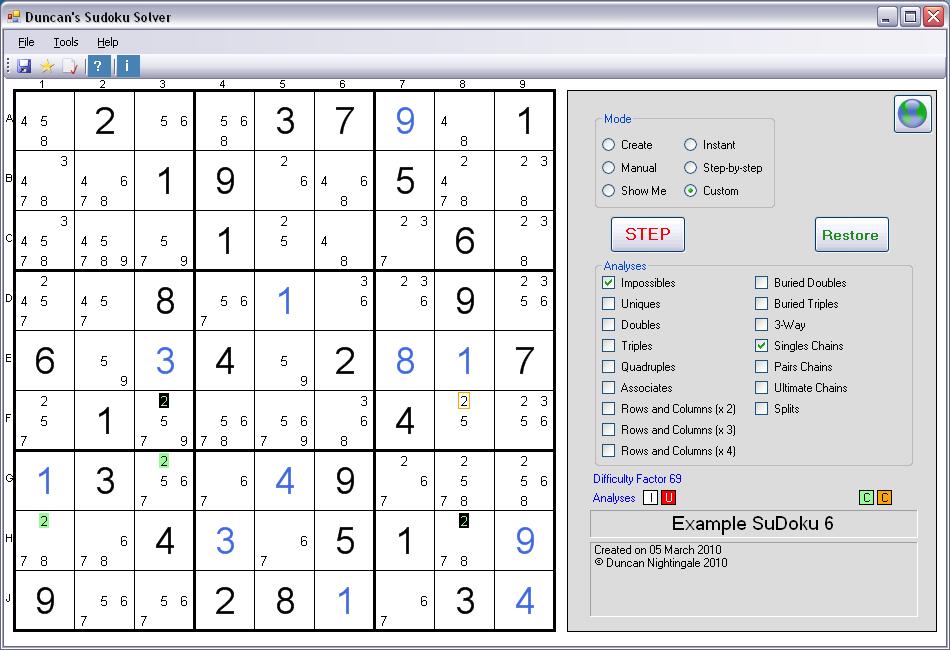
This is a screenshot
Singles Chain:
A linked Chain of single
Possibles.
The ends of the Chain (coloured black) and all the linking elements (coloured pale green) have the same value.
If one end of the Chain is 'false', then the other must be 'true' and vice-versa. Any Possible that can 'see' both ends of the Chain
may be removed.In this example, the Singles Chain is made up of 2's. The logic is as follows:
If the first end (F3) is NOT a 2,
the next link (G3) MUST be a 2
and the next link after that (H1) CANNOT be a 2
and then the other end of the chain (H8) MUST be a 2.
The 'MUST be' links are caused by there only being two 2's in the relevant Row, Column, or Box.
The 'CANNOT be' links are caused by the normal SuDoku rule that Solution values cannot be repeated in the same Row, Column, or Box.
All this means that if one end of the Chain is NOT a 2, the other end MUST be a 2 and vice-versa. Or, to put it another way, one or other of the ends is guaranteed to be a 2. So any Possible 2 that can 'see' both ends is an impossible solution (outlined in orange) and may be removed. For a Possible to 'see' another Possible, it must simply be in the same Row, Column, or Box and have the same value.
Second Example of a Singles Chain
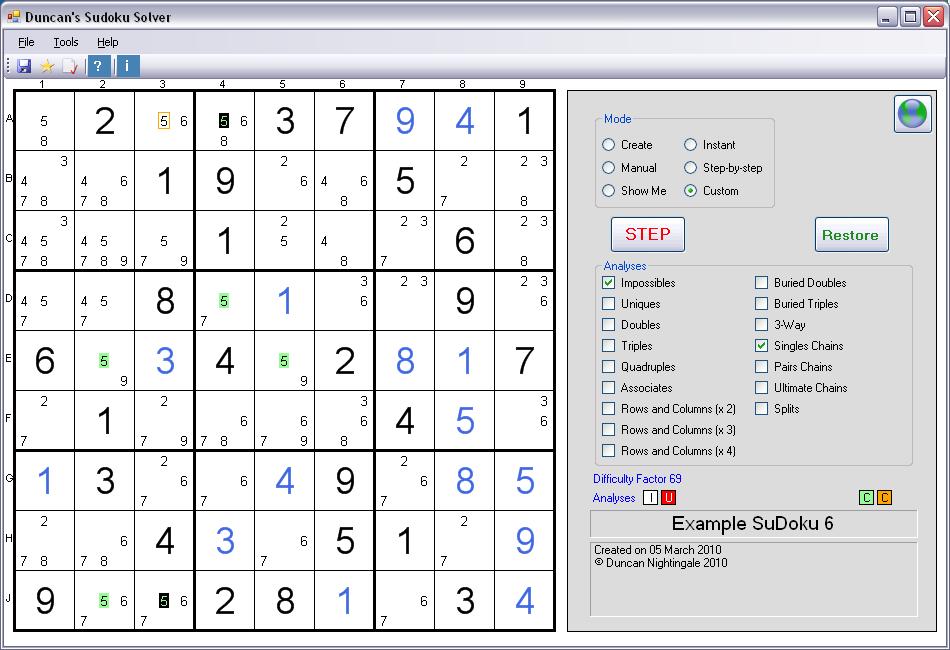
This is a screenshot
In this second example, the Singles Chain is made up of 5's. Once again, the Chain ends are coloured black
and the linking elements are coloured pale green. The logic is as follows:If the first end (A4) is NOT a 5,
the next link (D4) MUST be a 5
and the next link after that (E5) CANNOT be a 5
and the next link after that (E2) MUST be a 5
and the next link after that (J2) CANNOT be a 5
and then the other end of the chain (J3) MUST be a 5.
The 'MUST be' links are caused by there only being two 5's in the relevant Row, Column, or Box.
The 'CANNOT be' links are caused by the normal SuDoku rule that Solution values cannot be repeated in the same Row, Column, or Box.
All this means that if one end of the Chain is NOT a 5, the other end MUST be a 5 and vice-versa. Or, to put it another way, one or other of the ends is guaranteed to be a 5. So any Possible 5 that can 'see' both ends is an impossible solution (outlined in orange) and may be removed.