Example of a Diagonal
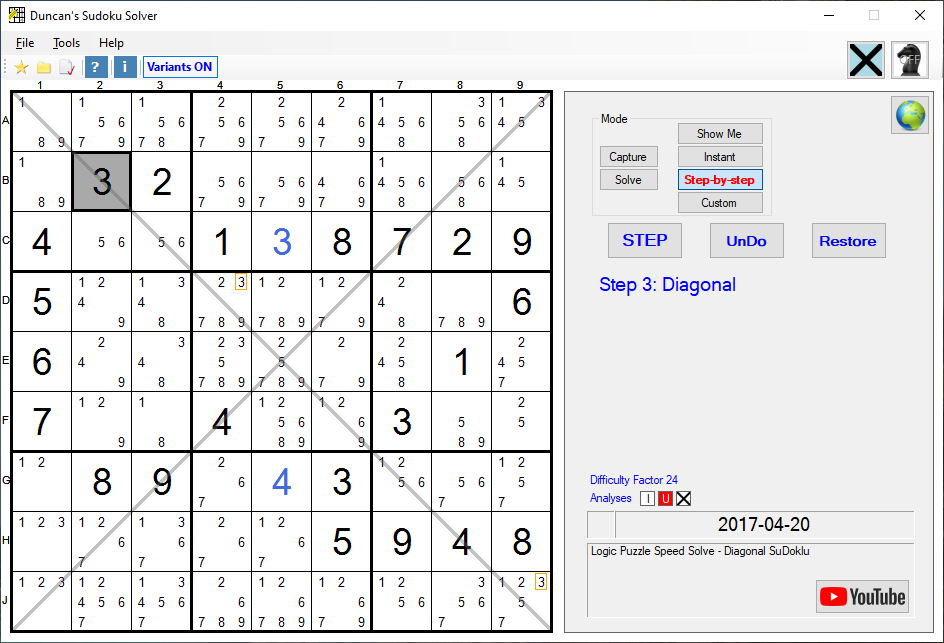
This is a version 13.0 screenshot
Diagonal:
The numbers 1 to 9 can only appear once on each of the Diagonals (marked in grey), in addition to the normal SuDoku rules of only appearing once in each Row, Column and Box. Because of the 3 on B2, the 3's in D4 and J9 (outlined in orange) are impossible solutions and can be removed.Second Example of a Diagonal
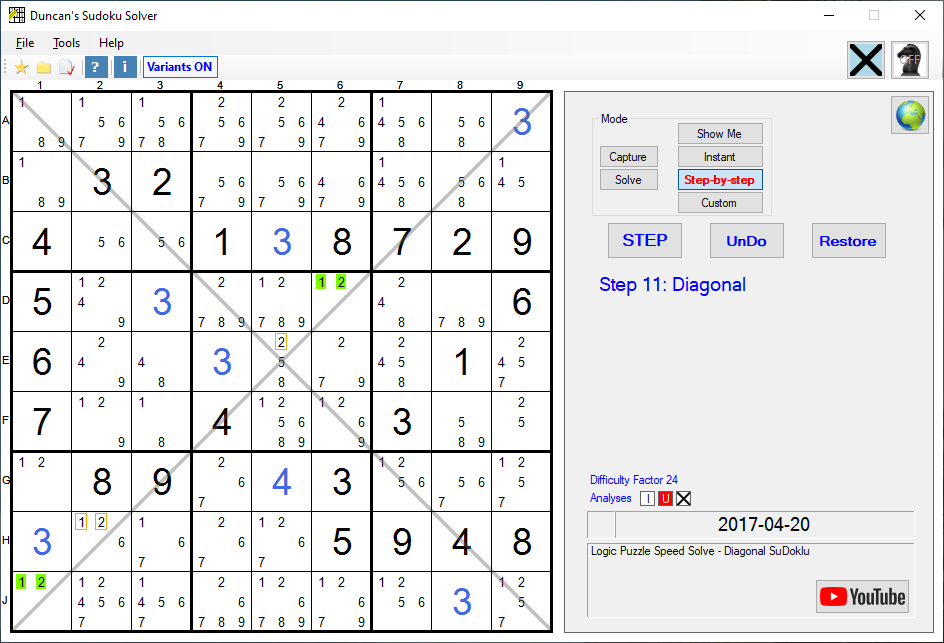
This is a version 13.0 screenshot
Diagonal:
In this second example, J1 and D6 form a Double of 1's and 2's (coloured green). These two Squares MUST contain 1 or 2. Therefore 1 and 2 cannot be in any other Square in the same Diagonal. The 1's and 2's on H2 and E5 (outlined in orange) are impossible solutions and can be removed.Third Example of a Diagonal
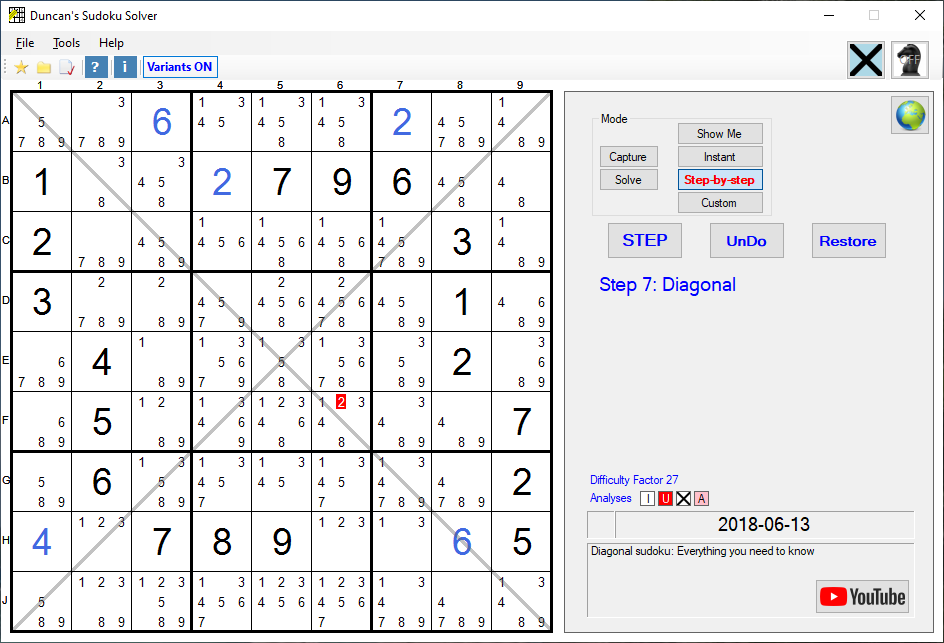
This is a version 13.0 screenshot
Diagonal:
In this third example, the 2 on F6 (coloured red) is the only remaining 2 on it's Diagonal, therefore it is a Unique and must be the Solution for F6.Fourth Example of a Diagonal
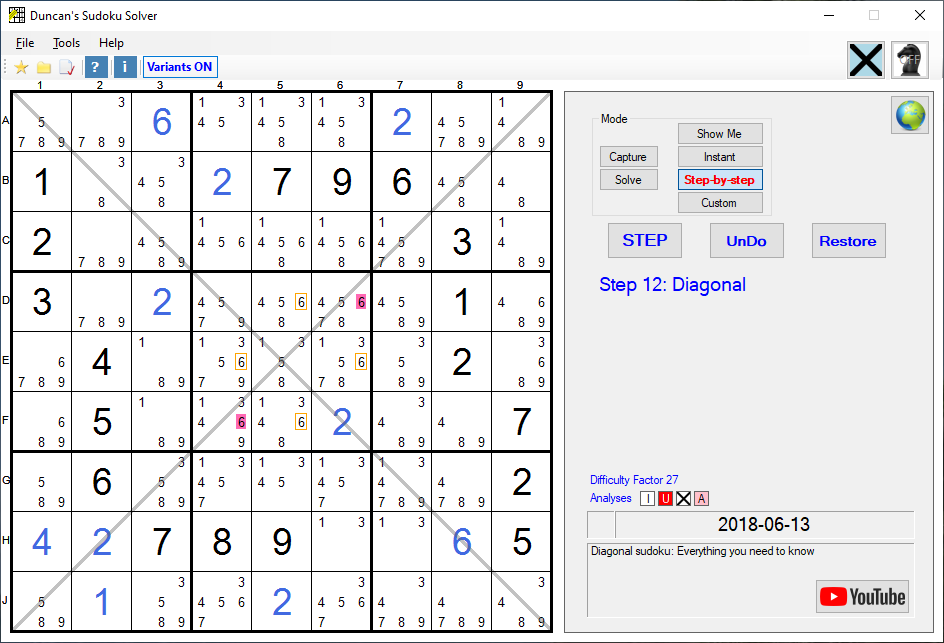
This is a version 13.0 screenshot
Diagonal:
In this fourth example, the 6's on F4 and D6 are the last two 6's on their Diagonal and are also contained within the same (central) Box. Therefore they comprise an Associate and the other 6's in the central Box (outlined in orange) are impossible solutions and may be removed.Fifth Example of a Diagonal
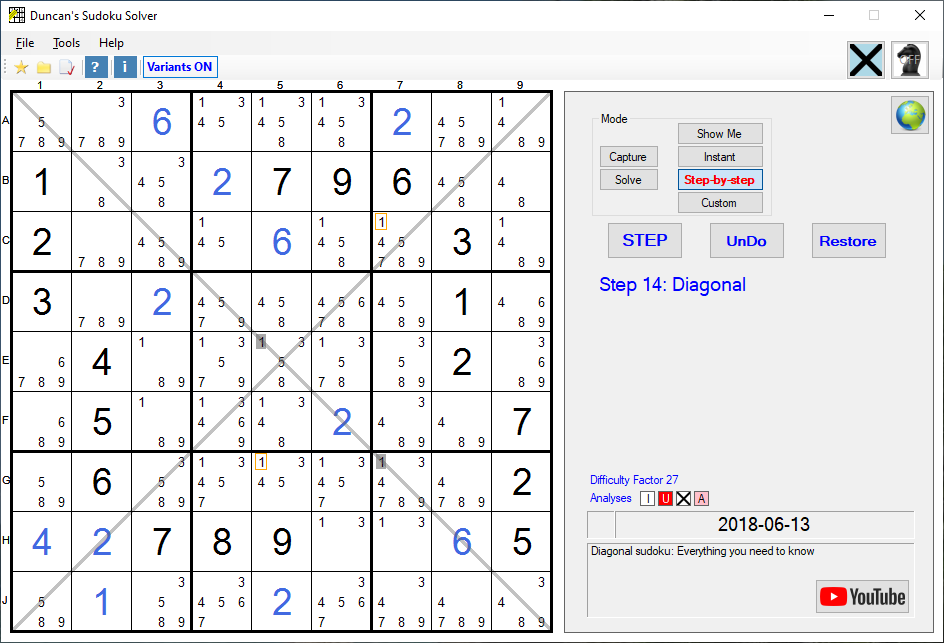
This is a version 13.0 screenshot
Diagonal:
In this fifth example, the 1's on E5 and G7 are the last two 1's on their Diagonal. Any Square that can 'see' both E5 and G7 cannot contain a 1. Therefore the 1's G5 and C7 (outlined in orange) are impossible solutions and may be removed.Sixth Example of a Diagonal
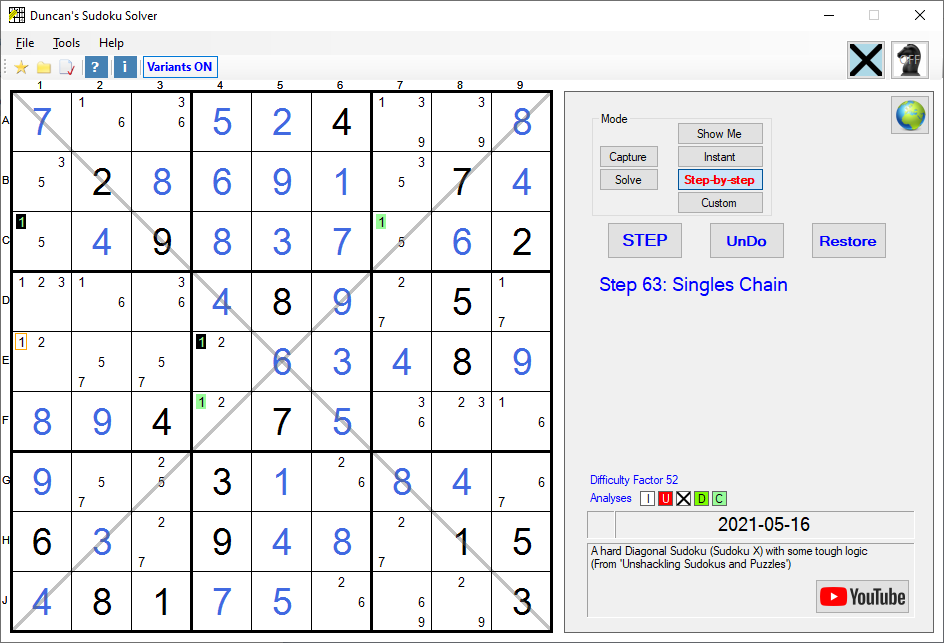
This is a version 13.0 screenshot
Diagonal:
Diagonals can also work with chains! In this sixth example, there is a Singles Chain in 1's. The end points (coloured black) are C1 and E4. Any Square that can 'see' both C1 and E4 cannot contain a 1. Therefore, the 1 on E1 (outlined in orange) is an impossible solution and can be removed. The logic is as follows:If the first end (C1) is NOT a 1,
the next link (C7) MUST be a 1
and the next link after that (F4) CANNOT be a 1
and then the other end of the chain (E4) MUST be a 1.
The 'MUST be' links are caused by there only being two 1's in the relevant Row, Column, Box, or Diagonal. The 'CANNOT be' links are caused by the normal SuDoku rule that Solution values cannot be repeated in the same Row, Column, Box, or Diagonal. All this means that if one end of the Chain is NOT a 1, the other end MUST be a 1 and vice-versa. Or, to put it another way, one or other of the ends is guaranteed to be a 1. So any Possible 1 that can 'see' both ends is an impossible solution (outlined in orange) and may be removed. For a Possible to 'see' another Possible, it must simply be in the same Row, Column, Box, or Diagonal and have the same value.